Skip to content

A Metric Learning Reality Check

This page contains additional information for the ECCV 2020 paper by Musgrave et al.

Optimization plots

Click on the links below to view the bayesian optimization plots. These are also available in the benchmark spreadsheet.

The plots were generated using the Ax package.

CUB200 Cars196 SOP CUB200 with Batch 256
Contrastive Contrastive Contrastive Contrastive
Triplet Triplet Triplet Triplet
NTXent NTXent NTXent NTXent
ProxyNCA ProxyNCA ProxyNCA ProxyNCA
Margin Margin Margin Margin
Margin / class Margin / class Margin / class Margin / class
Normalized Softmax Normalized Softmax Normalized Softmax Normalized Softmax
CosFace CosFace CosFace CosFace
ArcFace ArcFace ArcFace ArcFace
FastAP FastAP FastAP FastAP
SNR Contrastive SNR Contrastive SNR Contrastive SNR Contrastive
Multi Similarity Multi Similarity Multi Similarity Multi Similarity
Multi Similarity + Miner Multi Similarity + Miner Multi Similarity + Miner Multi Similarity + Miner
SoftTriple SoftTriple SoftTriple SoftTriple

Optimal hyperparameters

The values below are also available in the benchmark spreadsheet.

Loss function CUB200 Cars196 SOP CUB200 with Batch 256
Contrastive
pos_margin
neg_margin
-0.20001
0.3841
0.2652
0.5409
0.2850
0.5130
0.2227
0.7694
Triplet
margin
0.0961
0.1190
0.0451
0.1368
NTXent
temperature
0.0091
0.0219
0.0002
0.0415
ProxyNCA
proxy lr
softmax_scale
6.04e-3
13.98
4.43e-3
7.97
5.28e-4
10.73
2.16e-1
10.03
Margin
beta lr
margin
init beta
1.31e-3
0.0878
0.7838
1.11e-4
0.0781
1.3164
1.82e-3
0.0915
1.1072
1.00e-6
0.0674
0.9762
Margin / class
beta lr
margin
init beta
2.65e-4
0.0779
0.9796
4.76e-05
0.0776
0.9598
7.10e-05
0.0518
0.8424
1.32e-2
-0.0204
0.1097
Normalized Softmax
weights lr
temperature
4.46e-3
0.1087
1.10e-2
0.0886
5.46e-4
0.0630
7.20e-2
0.0707
CosFace
weights lr
margin
scale
2.53e-3
0.6182
100.0
7.41e-3
0.4324
161.5
2.16e-3
0.3364
100.0
3.99e-3
0.4144
88.23
ArcFace
weights lr
margin
scale
5.13e-3
23.22
100.0
7.39e-06
20.52
49.50
2.01e-3
18.63
220.3
3.95e-2
23.14
78.86
FastAP
num_bins
17
27
16
86
SNR Contrastive
pos_margin
neg_margin
regularizer_weight
0.3264
0.8446
0.1382
0.1670
0.9337
0
0.3759
1.0831
0
0.1182
0.6822
0.4744
Multi Similarity
alpha
beta
base
0.01
50.60
0.56
14.35
75.83
0.66
8.49
57.38
0.41
0.01
46.85
0.82
Multi Similarity + Miner
alpha
beta
base
epsilon
17.97
75.66
0.77
0.39
7.49
47.99
0.63
0.72
15.94
156.61
0.72
0.34
11.63
55.20
0.85
0.42
SoftTriple
weights lr
la
gamma
reg_weight
margin
5.37e-05
78.02
58.95
0.3754
0.4307
1.40e-4
17.69
19.18
0.0669
0.3588
8.68e-05
100.00
47.90
N/A
0.3145
1.06e-4
72.12
51.07
0.4430
0.6959

Examples of unfair comparisons in metric learning papers

Papers that use a better architecture than their competitors, but don’t disclose it

Papers that use a higher dimensionality than their competitors, but don’t disclose it

Papers that claim to do a simple 256 resize and 227 or 224 random crop, but actually use the more advanced RandomResizedCrop method

Papers that use a 256 crop size, but whose competitor results use a smaller 227 or 224 size

Papers that omit details

Examples to back up other claims in section 2.1

“Most papers claim to apply the following transformations: resize the image to 256 x 256, randomly crop to 227 x 227, and do a horizontal flip with 50% chance”. The following papers support this claim

Papers categorized by the optimizer they use

Papers that do not use confidence intervals

  • All of the previously mentioned papers

Papers that do not use a validation set

  • All of the previously mentioned papers

What papers report for the contrastive and triplet losses

The tables below are what papers have reported for the contrastive and triplet loss, using convnets. We know that the papers are reporting convnet results because they explicitly say so. For example:

  • Lifted Structure Loss: See figures 6, 7, and 12, which indicate that the contrastive and triplet results were obtained using GoogleNet. These results have been cited several times in recent papers.
  • Deep Adversarial Metric Learning: See tables 1, 2, and 3, and this quote from the bottom of page 6 / top of page 7: "For all the baseline methods and DAML, we employed the same GoogLeNet architecture pre-trained on ImageNet for fair comparisons"
  • Hardness-Aware Deep Metric Learning: See tables 1, 2, and 3, and this quote from page 8: "We evaluated all the methods mentioned above using the same pretrained CNN model for fair comparison."

Reported Precision@1 for the Contrastive Loss

Paper CUB200 Cars196 SOP
Deep Metric Learning via Lifted Structured Feature Embedding (CVPR 2016) 26.4 21.7 42
Learning Deep Embeddings with Histogram Loss (NIPS 2016) 26.4 N/A 42
Hard-Aware Deeply Cascaded Embedding (ICCV 2017) 26.4 21.7 42
Sampling Matters in Deep Embedding Learning (ICCV 2017) N/A N/A 30.1
Deep Adversarial Metric Learning (CVPR 2018) 27.2 27.6 37.5
Attention-based Ensemble for Deep Metric Learning (ECCV 2018) 26.4 21.7 42
Deep Variational Metric Learning (ECCV 2018) 32.8 35.8 37.4
Classification is a Strong Baseline for Deep Metric Learning (BMVC 2019) 26.4 21.7 42
Deep Asymmetric Metric Learning via Rich Relationship Mining (CVPR 2019) 27.2 27.6 37.5
Hardness-Aware Deep Metric Learning (CVPR 2019) 27.2 27.6 37.5
Metric Learning With HORDE: High-Order Regularizer for Deep Embeddings (ICCV 2019) 55 72.2 N/A

Reported Precision@1 for the Triplet Loss

Paper CUB200 Cars196 SOP
Deep Metric Learning via Lifted Structured Feature Embedding (CVPR 2016) 36.1 39.1 42.1
Learning Deep Embeddings with Histogram Loss (NIPS 2016) 36.1 N/A 42.1
Improved Deep Metric Learning with Multi-class N-pair Loss Objective (NIPS 2016) 43.3 53.84 53.32
Hard-Aware Deeply Cascaded Embedding (ICCV 2017) 36.1 39.1 42.1
Deep Metric Learning with Angular Loss (ICCV 2017) 42.2 45.5 56.5
Deep Adversarial Metric Learning (CVPR 2018) 35.9 45.1 53.9
Deep Variational Metric Learning (ECCV 2018) 39.8 58.5 54.9
Deep Metric Learning with Hierarchical Triplet Loss (ECCV 2018) 55.9 79.2 72.6
Hardness-Aware Deep Metric Learning (CVPR 2019) 35.9 45.1 53.9
Deep Asymmetric Metric Learning via Rich Relationship Mining (CVPR 2019) 35.9 45.1 53.9
Metric Learning With HORDE: High-Order Regularizer for Deep Embeddings (ICCV 2019) 50.5 65.2 N/A

Frequently Asked Questions

Do you have slides that accompany the paper?

Slides are here.

Isn't it unfair to fix the model, optimizer, learning rate, and embedding size?

Our goal was to compare algorithms fairly. To accomplish this, we used the same network, optimizer, learning rate, image transforms, and embedding dimensionality for each algorithm. There is no theoretical reason why changing any of these parameters would benefit one particular algorithm over the rest. If there is no theoretical reason, then we can only speculate, and if we add hyperparameters based on speculation, then the search space becomes too large to explore.

Why did you use BN-Inception?

We chose this architecture because it is commonly used in recent metric learning papers.

Why was the batch size set to 32 for most of the results?

This was done for the sake of computational efficiency. Note that there are:

  • 3 datasets
  • 14 algorithms
  • 50 steps of bayesian optmization
  • 4 fold cross validation

This comes to 8400 models to train, which can take a considerable amount of time. Thus, a batch size of 32 made sense. It's also important to remember that there are real-world cases where a large batch size cannot be used. For example, if you want to train on large images, rather than the contrived case of 227x227, then training with a batch size of 32 suddenly makes a lot more sense because you are constrained by GPU memory. So it's reasonable to check the performance of these losses on a batch size of 32.

That said, there is a good theoretical reason for a larger batch size benefiting embedding losses more than classification losses. Specifically, embedding losses can benefit from the increased number of pairs/triplets in larger batches. To address this, we benchmarked the 14 methods on CUB200, using a batch size of 256. The results can be found in the supplementary section (the final page) of the paper.

Why weren't more hard-mining methods evaluated?

We did test one loss+miner combination (Multi-similarity loss + their mining method). But we mainly wanted to do a thorough evaluation of loss functions, because that is the subject of most recent metric learning papers.

For the contrastive loss, why is the optimal positive margin a negative value?

A negative value should be equivalent to a margin of 0, because the distance between positive pairs cannot be negative, and the margin does not contribute to the gradient. So allowing the hyperparameter optimization to explore negative margins was unnecesary, but by the time I realized this, it wasn't worth changing the optimization bounds.

In Figure 2 (papers vs reality) why do you use Precision@1 instead of MAP@R?

None of the referenced papers report MAP@R. Since Figure 2a is meant to show reported results, we had to use a metric that was actually reported, i.e. Precision@1. We used the same metric for Figure 2b so that the two graphs could be compared directly side by side. But for the sake of completeness, here's Figure 2b using MAP@R:

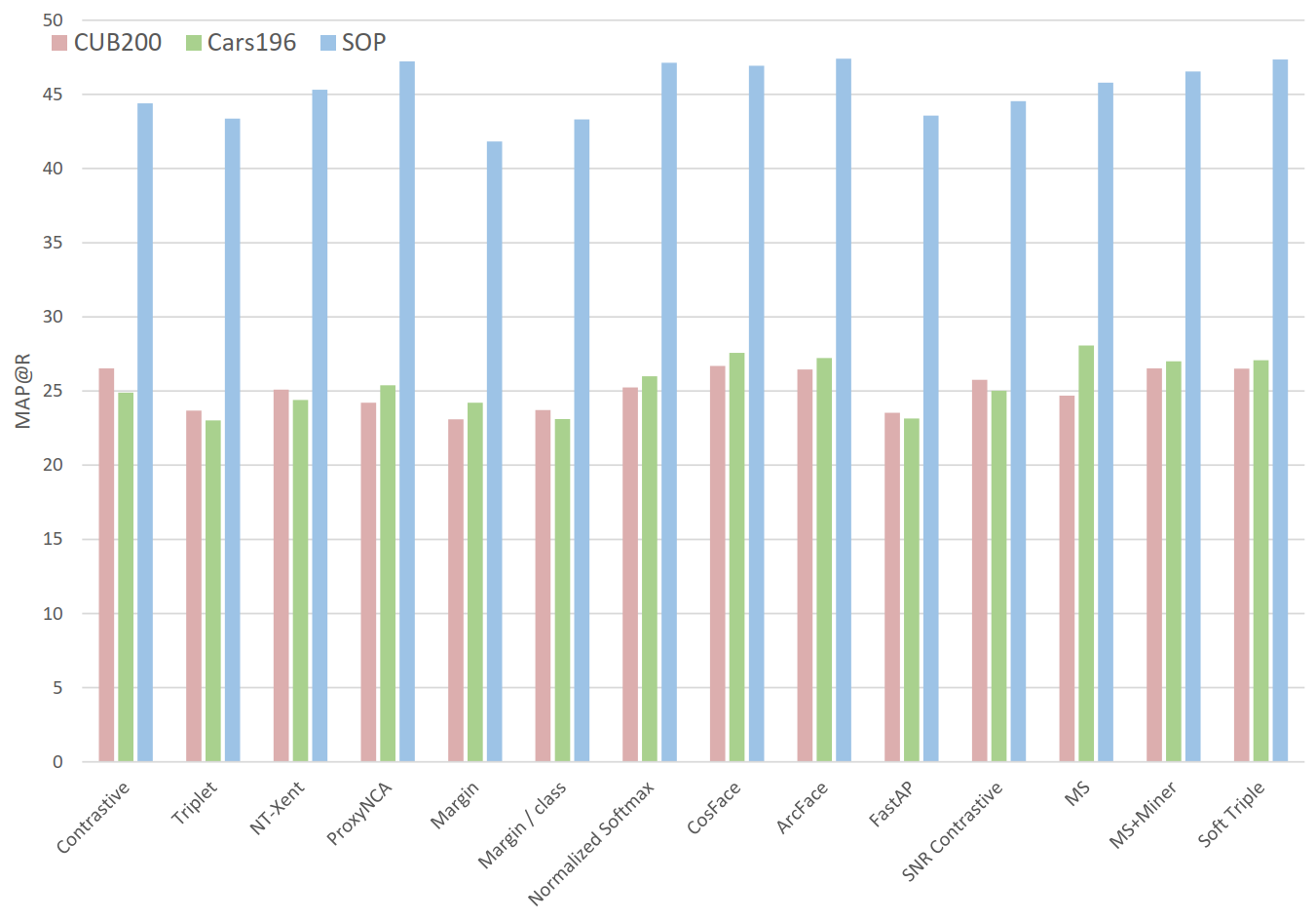
reality_over_time_mapr

Reproducing results

Install the compatible version

Please install version 0.9.32:

pip install powerful-benchmarker==0.9.32

Download the experiment folder

  1. Download run.py and set the default flags
  2. Go to the benchmark spreadsheet
  3. Find the experiment you want to reproduce, and click on the link in the "Config files" column.
  4. You'll see 3 folders: one for CUB, one for Cars, and one for SOP. Open the folder for the dataset you want to train on.
  5. Now you'll see several files and folders, one of which ends in "reproduction0". Download this folder. (It will include saved models. If you don't want to download the saved models, go into the folder and download just the "configs" folder.)

Command line scripts

Normally reproducing results is as easy as downloading an experiment folder, and using the reproduce_results flag. However, there have been significant changes to the API since these experiments were run, so there are a couple of extra steps required, and they depend on the dataset.

Additionally, if you are reproducing an experiment for the Contrastive, Triplet, or SNR Contrastive losses, you have to delete the key/value pair called avg_non_zero_only in the config_loss_and_miners.yaml file. And for the Contrastive loss, you should delete the use_similarity key/value pair in config_loss_and_miners.yaml.

In the following code, <experiment_to_reproduce> refers to the folder that contains the configs folder.

  • CUB200:
python run.py --reproduce_results <experiment_to_reproduce> \
--experiment_name <your_experiment_name> \
--split_manager~SWAP~1 {MLRCSplitManager: {}} \
--merge_argparse_when_resuming
  • Cars196:
python run.py --reproduce_results <experiment_to_reproduce> \
--experiment_name <your_experiment_name> \
--config_dataset [default, with_cars196] \
--config_general [default, with_cars196] \
--split_manager~SWAP~1 {MLRCSplitManager: {}} \
--merge_argparse_when_resuming
  • Stanford Online Products
python run.py --reproduce_results <experiment_to_reproduce> \
--experiment_name <your_experiment_name> \
--config_dataset [default, with_sop] \
--config_general [default, with_sop] \
--split_manager~SWAP~1 {MLRCSplitManager: {}} \
--merge_argparse_when_resuming
  • CUB200 with batch size 256:
python run.py --reproduce_results <experiment_to_reproduce> \
--experiment_name <your_experiment_name> \
--config_general [default, with_256_batch] \
--split_manager~SWAP~1 {MLRCSplitManager: {}} \
--merge_argparse_when_resuming

If you don't have the datasets and would like to download them into your dataset_root folder, you can add this flag to the CUB commands:

--dataset~OVERRIDE~ {CUB200: {download: True}}

Likewise, for the Cars196 and Stanford Online Products commands, replace the --config_dataset flag with:

--dataset~OVERRIDE~ {Cars196: {download: True}}

or 

--dataset~OVERRIDE~ {StanfordOnlineProducts: {download: True}}

Run evaluation on the test set

After training is done, you can get the "separate 128-dim" test set performance:

python run.py --experiment_name <your_experiment_name> \
--evaluate --splits_to_eval [test]

and the "concatenated 512-dim" test set performance:

python run.py --experiment_name <your_experiment_name> \
--evaluate_ensemble --splits_to_eval [test]

Once evaluation is done, you can go to the meta_logs folder and view the results.

Using the trained models outside of powerful-benchmarker

If you want to use the trained models in your own code, here are the steps:

1. Load the models (after you've downloaded them)

import pretrainedmodels # needs to be installed with pip
from pytorch_metric_learning.utils import common_functions as c_f
from powerful_benchmarker import architectures
import torch

trunk = pretrainedmodels.bninception()
trunk.last_linear = c_f.Identity()
embedder = architectures.misc_models.MLP([1024, 128])

trunk.load_state_dict(torch.load("trunk_best.pth"))
embedder.load_state_dict(torch.load("embedder_best.pth"))

2. Apply the correct transforms

Make sure to apply the ConvertToBGR and Multiplier transforms, and use the correct mean and std in the Normalize transform:

from PIL import Image
from torchvision import transforms

class ConvertToBGR(object):
    """
    Converts a PIL image from RGB to BGR
    """

    def __init__(self):
        pass

    def __call__(self, img):
        r, g, b = img.split()
        img = Image.merge("RGB", (b, g, r))
        return img

    def __repr__(self):
        return "{}()".format(self.__class__.__name__)


class Multiplier(object):
    def __init__(self, multiple):
        self.multiple = multiple

    def __call__(self, img):
        return img*self.multiple

    def __repr__(self):
        return "{}(multiple={})".format(self.__class__.__name__, self.multiple)


transform = transforms.Compose([ConvertToBGR(),
                                transforms.Resize(256), 
                                transforms.CenterCrop(227), 
                                transforms.ToTensor(),
                                Multiplier(255),
                                transforms.Normalize(mean = [104, 117, 128], 
                                                     std = [1, 1, 1])])